Author: joshwilkerson

Corpus Hypercubus

joshwilkerson1 Comment

Courtesy of the Association of Christians in the Mathematical Sciences:

Salvador Dali’s painting Corpus Hypercubus (1954) is a fascinating visual representation of a mathematical metaphor for the theological mystery of crucifixion.

Corpus Hypercubus, Salvador Dali (1954)

Many people are familiar with how to unfold a cube from three dimensions into two as shown in the figures below. Some of the edges of the cube are separated so that the resulting collection of squares can be unfolded into a planar shape. The resulting diagram is called a “net” for the cube. The net is not unique but one common net resembles a cross.

Dali painted the cross in Corpus Hypercubus as a hypercube unfolded into 3-dimensional space. The hypercube consists of eight three-dimensional cubes for hyperfaces. Each hyperface is attached along a two-dimensional square face to six of the other hyperfaces. Just as one can unfold a cube, one can also unfold a hypercube into the shape depicted in Dali’s painting.

Using the analogy of a (mysterious) higher-dimensional object unfolded into three dimensions, Dali depicts the theological mystery of the crucifixion as an event that originated in a higher plane of existence and then unfolded into the world that we perceive. With this understanding, Corpus Hypercubus communicates the idea that though one can discuss the necessity of the Jesus’ sacrifice for salvation or study theological ramifications of the cross, one can only do so by analogy because human nature simply cannot perceive the scope of God’s plan.

More from the ACMS:

Mathematical Affections: Assessing Values in the Math Classroom

joshwilkersonLeave a comment

I will be speaking on “Mathematical Affections: Assessing Values in the Math Classroom” at the 2013 ACMS Conference. Here is the abstract for the talk:

“When am I ever going to use this?” As a math teacher, this is the number one question that I hear from students. It is also a wrong question; it isn’t the question the student truly intended to ask. The question they are really asking is “Why should I value this?” and they express their inquiry in terms of practicality because that is the language in which their culture has conditioned them to speak. While the utility of mathematical concepts are certainly important, we as educators need to utilize the mathematics classroom to address the more fundamental issue of fostering a proper sense of values. Learning has little meaning unless it produces a sustained and substantial influence on the way people think, act, feel, and ultimately worship. According to the NCTM standards it is through assessment that we most clearly communicate to students what aspects of mathematics are to be valued. This talk will address two essential questions:

1) Why is it necessary to develop assessments that equip students to not only know and practice but also love that which is true, good and beautiful?

2) How do we design worthwhile mathematical assessments that synthesize something seemingly non-objective like personal values with something seemingly non-subjective like mathematics?

The title of this talk is in homage to Jonathan Edwards’ Treatise on Religious Affections. Edwards’ goal was to discern the true nature of religion and in so doing dissuade his congregation from merely participating in a Christian culture (a mimicked outward expression) and motivate them to long for true Christian conversion (an inward reality of authentic Christian character). The purpose of this talk is to engage ACMS members in discerning the true nature of mathematical assessment and how we use it in the classroom: does it simply mimic the modern culture of utility by requiring outward demonstrations of knowledge retention and application, or does it aim deeper at analyzing true inward character formation? In closing, examples of affective mathematical assessments will be presented as resources for consideration and classroom use.

I also have the honor of serving as a panel member for a session on service-learning organized by Dr. Karl-Dieter Crisman of Gordon College. Here is the abstract on that talk:

Many of us have wanted to incorporate service experiences in courses, or are being asked by our institutions to do so. Service-learning is a way of looking at service as being a partner with and leading to learning for our students. But in math, there are not a lot of resources to use! Our panelists will present classroom-tested ideas from several different levels of course, and we will end with a short time for more brainstorming among all participants.

I will share more details on both of these talks as the conference draws near. For now, here are links to some related posts on GodandMath.com as well as other sites:

PRIMUS and Service-Learning

Serving Through Statistics

CAMT 2012 Presentation

God, Math, and Order

Service-Learning Session from 2011 Joint Math Meetings (Organized by Dr. Crisman)

Aims for Christian Math Education

joshwilkersonLeave a comment

By Steve Bishop

(Disclaimer: The views expressed by guest authors do not necessarily reflect those of GodandMath.com. Guest articles are sought after for the purpose of bringing more diverse viewpoints to the topics of mathematics and theology. The point is to foster discussion. To this end respectful and constructive comments are highly encouraged.)

It has been said that the most incomprehensible thing about the world is its comprehensibility. Mathematics is only possible because God has created an ordered, law-full, universe that is comprehensible. Part of the task of mathematics is to describe the wonder of God’s good creation and thereby reveal some of the invisible attributes of God e.g. his faithfulness. Mathematics is also integral to the fulfilling of the creation mandate to open up and develop the creation. Mathematics is an important tool to help us steward and unfold the potentialities of the earth. Music, art, science and economics are four subjects that would be severely impoverished without the aid of mathematics.

Mathematics is a collective term for a number of related fields: arithmetic, geometry, topology, statistics, probability, … . All of which investigate and open up the two most basic aspects of reality: the numerical and spatial. (Applied mathematics also deals with a third aspect: the kinematic).

Math is a human activity therefore, it comes replete with human limitations: it is fallible, corrigible, culture- and value-laden. However, it is based in creation – it is not arbitrary or the product of social agreement. This is where a Christian view of math diverges from the social constructivist view. This Christian view of math does justice to both epistemological subjectivity and ontological objectivity.

Mathematics is based in created reality. It is not neutral; religious beliefs shape mathematical theories.

Mathematical Education Aims

Hence, mathematics education should:

1. Be placed in a historical and cultural context.
This will help to expose the myth of mathematical objectivity.

2. Be rooted in reality and everyday applications.
This will help show mathematics as a tool for unfolding and developing the creation.

3. Be integrated with other subjects.
Mathematics deals with the two most basic aspects of reality, the numerical and the spatial, these aspects are basic to all other curriculum subjects. The integration with other subjects, particularly science, reveals the role of mathematics as a tool to help fulfill the cultural mandate.

4. Describe the beauty and order of creation and to help students understand creation.

5. Reveal some of the attributes of God (Rom 1:20; Ps 19:1). Particularly the faithfulness of God to His creation exemplified in His laws and the lawfulness of creation. Without this mathematics would be impossible.

6. Enable us the be better stewards of God’s creation.

7. Provide fun and enjoyment.

8. Focus on understanding rather than rote or memorization.

9. Recognize that each student is created in God’s image and that each student is unique.
Differentiation will be important.  We all learn in different ways and at different rates, this should be taken into account.

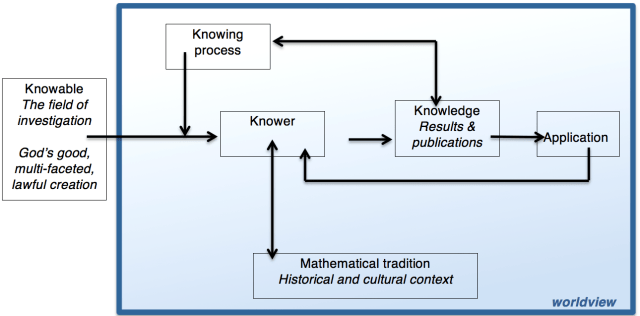
A model for mathematics – all activity takes place within a worldview. Hence epistemological subjectivity, but ontological objectivity. History and application play important roles (Adapted from an original diagram by Revd Richard Russell.)

Steve Bishop is the compiler of A Bibliography for a Christian Approach to Mathematics and the author of several articles on the relationship between faith and math, including his series on Christian Mathematicians here at GodandMath.com.