by Pete Downing
This article was originally published on bethinking.org and is being republished here with permission. Please feel free to contact Pete (PDowning@uccf.org.uk) if you want to discuss any of the ideas presented here in more detail.
‘Another calculus lecture drifts by, and I still don’t understand how my faith in Jesus has got anything to do with the hours upon hours I spend every week learning more about maths.’ This is the experience of so many Christians in the world of maths, as we find it hard to see how our faith relates to our subject. So, what has the God of the Bible got to do with maths? What has maths got to do with the Christian gospel?
As we begin, it’s important to acknowledge that we are not trying to represent a Christian view on maths here, but rather we are trying to understand the reality of maths. What we are looking at is not simply our perspective as Christians, it is the true reality revealed to us by the God of the universe.
The Lord of maths
Let’s begin with what the apostle Paul says about Jesus in Colossians 1:15–20:
The Son is the image of the invisible God, the firstborn over all creation. For in him all things were created: things in heaven and on earth, visible and invisible, whether thrones or powers or rulers or authorities; all things have been created through him and for him. He is before all things, and in him all things hold together. And he is the head of the body, the church; he is the beginning and the firstborn from among the dead, so that in everything he might have the supremacy. For God was pleased to have all his fullness dwell in him, and through him to reconcile to himself all things, whether things on earth or things in heaven, by making peace through his blood, shed on the cross.
Jesus Christ has the supremacy over everything that exists – and that includes maths. Jesus is supreme over maths, he was the one who thought it all up, and he cares about those things that you care about and get excited by. Jesus is the Lord of all, Jesus is the Lord of maths. I wonder how that makes you feel?
So, as Jesus is the Lord of maths, it follows that how we conduct ourselves as we study maths is very important. As human beings either we worship the Creator (God) because of created things, or we worship the created things themselves (Romans 1:18–25). There is no ground in between. So we either do maths for God’s glory, to show the greatness of God who created it in all its beauty and who gave us the brains to be able to understand it. Or we do maths for our own glory, to show the greatness of our own human intellect. And only one of these rightly recognizes Jesus’ lordship over maths!
The nature of maths
Let’s assume that mathematical objects do indeed exist. I would guess that most of us as mathematicians do believe this, which raises the important question: How do mathematical objects exist? If you are an atheist, then you’ve got a serious problem in answering this question. For when and how did they come into being without a creator? But as Christians, we have a very convincing answer to this: Mathematical objects exist in the mind of God.
This conclusion flows naturally from the Bible’s teaching about the nature of God. For example, John’s Gospel says ‘In the beginning was the word’ (John 1:1). The Greek term translated as ‘word’ here is λόγος (logos), but the range of meaning of λόγος is much broader and deeper than this. It combines notions like ‘reason’, ‘wisdom’, ‘speech’. In fact, our modern word ‘logic’ is derived from this Greek word. So, in the beginning was the λόγος (which includes maths), and the λόγος was with God, and the λόγος was God. Importantly, the λόγος is not an abstract concept or a particular quality in the mind of God, but rather is a person – Jesus Christ. The same Jesus that we saw in Colossians 1 who has the supremacy over all things. In him, through him, and for him all things were created, and these things express the mathematical objects that have existed from the beginning, in the mind of God.[1]
Taking this further, the Bible tells us that God rules his world through his speech: ‘By the word of the Lord the heavens were made, and by the breath of his mouth all their host’ (Psalm 33:6). His word also sustains his creation: ‘He upholds the universe by the word of his power’ (Hebrews 1:3).
The theologian Vern Poythress helpfully expands:
God’s word has divine wisdom, power, truth, and holiness. It has divine attributes, because it expresses God’s own character. God expresses rather than undermines his own deity when he speaks words that address the created world.
We may then conclude that the same principle applies in particular to numerical truths about the world. God governs everything, including numerical truth. His word specifies what is true. The apples in a group of four apples are created things. What God says about them is divine. In other words, his word specifies that 2 + 2 = 4.[2]
The usefulness of maths
And what about the interaction of mathematical objects with the physical world around us? How is it possible that sophisticated mathematical objects (like PDEs, infinite Hilbert spaces, complex numbers) which are abstract and have no causal relationship to the physical world, describe the universe with such astonishing accuracy? Again, if you are an atheist, then you’ve got a serious problem. Here are two quotes from ‘The unreasonable effectiveness of mathematics in the natural sciences’ by mathematician Eugene Wigner (an atheist):
[The] enormous usefulness of mathematics in the natural sciences is something bordering the mysterious and there is no rational explanation for it.
The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve.[3]
Did you notice how Wigner needs to resort to concepts clearly outside the boundaries of science like ‘the mysterious’ or ‘miracle’ to explain a fundamental fact of scientific research? For him, there is no rational explanation for the fact that maths can be used in physics. But if God created the universe, then we should expect to find evidence of his action in the physical world. The Bible makes that claim over and over again (e.g. Romans 1:20; Psalm 19:1; Isaiah 40:26). The physical world can be described so well by mathematics because this is precisely the language in which it was written by God, in whose mind mathematics exists.
The complexity of maths
Let’s now briefly consider the complexity of the equation: 2 + 2 = 4. As we will see, it is far more complicated that it seems on the surface.
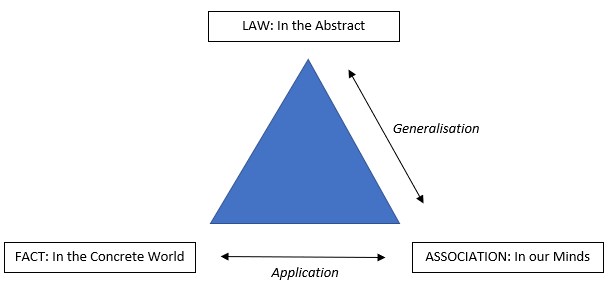
In maths we are really dealing with three realms:
- The abstract laws, which are the most general statements (2 + 2 = 4). You can’t touch it or feel it, you can’t experience it, you can only know it.
- The concrete instances of the laws which we call facts. Such as 2 apples + 2 apples = 4 apples.
- The association between Law and Fact. This really happens in our minds and is the most mysterious. It is what we use when we generalize (more abstract) or apply (more concrete). This is what a child does when he/she realizes that you don’t need to build a new arithmetic to count oranges when you know how to count apples.
And this poses the question: How is it possible that the human mind can discover and understand mathematics, which is abstract and has no causal relationship to the physical world? How is it that we are able to use association to relate the law and the facts?
(Note from GodandMath: for more on this point see “Why Math Works” by John Mays)
As human beings each one of us are created in the image of God (Genesis 1:27). So, we all reflect the characteristics of God, including our capacity to love, speak, reason and to do maths, art, or music. And so, it makes perfect sense that as human beings we can discover and understand maths, because maths is in the mind of God. We are made in his image, and this includes the privilege of thinking his thoughts after him.
What is the link between the three realms then? The non-believer cannot answer this question. For the Christian, God as creator is sovereign over all three realms; he has thought the laws, created the facts and made us in his image so that we can ‘join the dots’.
Principles for the Christian mathematician
I wonder why you decided to study maths? Unlike a lot of subjects, people don’t usually study maths to prepare for a specific career or because they hope to earn loads of money. Normally it’s either because they are good at it or because they enjoy the sheer beauty of it. Two things are worth noting off the back of this:
Mathematicians love maths
Which is kind of weird when you think about it, we love an abstract object that is not part of the physical world… How do we explain an intelligent human being leaping for joy just because of a neat result or proof? Well, if doing maths is thinking God’s thoughts after him, then doing maths has a lot to do with worship. We are called to worship God and rejoice in him. If mathematical objects exist in the mind of God, then discovering mathematical truths means in some way getting to know our Creator better. And that is what we are created to do. So, as Christian mathematicians, let’s continue to enjoy the beauty of maths knowing that it displays the beauty of God. And when we do maths, let’s do it as an act of worship to him.
Mathematicians struggle with maths
Understanding mathematical concepts is just hard! If you are studying maths, then you will know the common pattern of problem sets. You begin looking at question 1 and have no idea what to do. So, you move on to question 2, and again have no idea what to do. The same thing happens with question 3. But you have to start somewhere, and so you spend hours dissecting your lecture notes and trying to work out how on earth to begin. Perhaps even resorting to asking Google. But the sobering fact is that often you will just suddenly just get the answer, and it is really short and simple. If you go on to do research in maths, the phenomenon happens in a similar way (so I’m told). No progress on a problem for months, and then one afternoon it can all just fall into place!
The frustration that we experience while doing maths points to the fact that we are fallen human beings. We can’t think God’s thoughts after him the way it should be. But there are wonderful moments of grace, gifts from God, where he opens our eyes so that we can indeed think his thoughts after him in the way that he made us to. Those moments are wonderful gifts from God, and it is right that we thank him for them.
With these things in mind, it would be helpful for us to search our hearts to assess what our heart attitude towards our mathematical studies is and how we live that out. What is my motivation for studying maths? What is driving the goals that I set myself in my studies? Do I take pride in my work to the extent that I treat it as my own discovery rather than God revealing truth to me? As a Christian, should my work look different? These are not simple questions and require significant thought.
As mathematicians, we have the privilege of thinking God’s thoughts after him, and so in understanding maths more in some small way we get to understand our Creator more. We are not making discoveries of our own, but God is revealing the truth of his creation to us, and so it is our joy and delight to be able to help others to see and enjoy that too. It’s not our secret to keep hidden. And perhaps our solutions don’t look hugely different on the page, but they certainly do in our heart attitudes towards them, let’s give glory and praise to God as we work through our problem sets and understand more about how he has created and sustains the world.
Suggested Reading
- Vern S. Poythress, Redeeming Mathematics: A God-centred approach to mathematics (Crossway, 2015). Available as a free PDF from the author’s website.
- Vern S. Poythress, ‘A Biblical View of Mathematics’ in Gary North, ed., Foundations of Christian Scholarship (Ross House Books, 1979).
- Vern S. Poythress, various articles on mathematics.
References
[1] This is not a fully fleshed out argument of this point, which would require much more space than is available here. For those who are interested to explore it further, parts I & II of Redeeming Mathematics help to tackle that question at length.
[2] Vern S. Poythress, Redeeming Mathematics (Crossway, 2015) p.20 (emphasis in original).
[3] Wigner, E. P. ‘The unreasonable effectiveness of mathematics in the natural sciences’ Communications on Pure and Applied Mathematics, 13.1 (1960), 1–14
