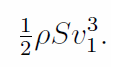Author: joshwilkerson

The Myth of Critical Thinking in Mathematics

joshwilkerson5 Comments

One of the most touted reasons for the necessity of every student undertaking mathematics courses in school (regardless of their ability or interest level in the subject) is that math teaches students critical thinking skills. I hate to burst bubbles here (actually I don’t) but this claim is completely and utterly false. Critical thinking in mathematics is a myth.

To “think critically” is by definition “to be critical of thoughts” or in other words “to critique ideas” as they arise rather than accepting or rejecting them blindly. Critical thinking means thinking rationally and reasoning through arguments with care and consideration of the options on the table. This, of course, sounds all well and good until we as educators stop and actually consider the reality of the situation in the math classroom. 

A critique can only be meaningful if you already have a standard by which to judge something. I can’t critique an argument as “true” unless I know what it means for something to be “true.” I can’t critique a painting as “beautiful” unless I know hat it means to be “beautiful.” I can’t critique an act of charity as “good” unless I know what it means to be “good.”

There is an underlying standard of judgment that is being instilled in students (whether knowingly or unknowingly) and this is the root of what is occurring in mathematics classrooms. The way in which students implement their “critical thinking skills” upon the completion of their mathematics courses is simply a symptom of a deeper reality that is being formed within them. That reality can be formed from a Christian perspective where it is God who sets the absolute standards for Truth, Beauty and Goodness, or it can be formed by very humanistic standards of relative truth, subjective beauty, and goodness defined by utility.

I submit to you that there is an opportunity present before us as math educators to impact the very standards by which students judge their thinking. This is the goal we should ultimately be aiming for. Don’t settle for simply teaching “critical thinking” skills.

They are just a myth.

How to Fall in Love with Math

joshwilkerson1 Comment

I’ve written before about the need to focus on the affective side of learning mathematics. It is a topic I am quite passionate about and it is the focus of my Ph.D. research in math education. I feel strongly enough about it that when people ask me what I teach I don’t respond with “I teach math,” or “I teach geometry,” or “I teach statistics.” Rather, I respond with “I teach math appreciation.” I think that is a much more apt description of our calling as math educators. We love math and the majority of students do not. Our goal is not to simply transfer our intellectual knowledge to the students, but to infect them with out enthusiasm.

I have been encouraged to see a recent publication come to my attention that address this matter. It was a New York Times article titled “How to Fall in Love with Math.” While I don’t necessarily agree with the conclusion of the article, that the solution to the problem is to be found in technology, it is nice to see the problem of mathematical affections being raised in the first place. I also enjoyed the opening of the article where the author clearly states what every math educator knows that nobody else does: when people say things like “do the math” they reveal that the public perception is that mathematics and arithmetic are the same thing. In reality arithmetic is an extremely small subset of mathematics. Mathematics as a discipline has something much grander than simply addition and multiplication that propels it forward. As the author states:

As a mathematician, I can attest that my field is really about ideas above anything else. Ideas that inform our existence, that permeate our universe and beyond, that can surprise and enthrall.

Creation Care as a Focus for a General Mathematics Course

joshwilkerson3 Comments

By Dr. John Roe, Penn State University

The following is from a talk given by Dr. John Roe at the ACMS Conference this past June. It is with his gracious permission that I am sharing it here. I invite you to check out Dr. Roe’s blog “Points of Inflection.”

1. INTRODUCTION

Christian higher education institutions typically expect their faculty members to demonstrate “the integration of faith and learning” in their classrooms. (While the specific language of “integration” is most characteristic of the Reformed tradition, a requirement to exhibit some kind of wholeness between academic subject-matter and faith commitments is both natural and widespread.) Some subjects seem to lend themselves to such “integration” more easily than others—philosophy or history or even economics, for instance, seem to lie closer to traditional faith concerns than mathematics. Indeed, it may seem that mathematics is one of the toughest nuts for the would-be “faith and learning integrator” to crack!

In his article on mathematics in [9], Harold Heie expresses his strategy for initiating students into the integrative project as follows:

The goal of initiation requires that I help students see that the worldview project is worthwhile. That is much easier said than done. How does a teacher do that? A strategy that I have found to work, some of the time, is to pose an integrative question. By “integrative question” I mean a question that cannot be addressed adequately without formulating coherent relationships between academic disciplinary knowledge and biblical/theological knowledge.

Various kinds of integrative questions have been proposed int the mathematical realm. For instance, one could ask questions like:

  • What is the nature of mathematical objects. Are they created or discovered? In what ways is it appropriate to say that mathematics provides the “laws” of God’s creation? (ontological and epistemological).
  • Can mathematical insights provide analogies to help us understand theological truths? Is the deductive method of the mathematician useful for defending the Christian faith? (apologetic). This is Heie’s own proposal.
  • What does it mean to practise mathematics ethically? What are the values informing the practice of mathematics? In what ways can they support, and in what ways can they conflict with, other values?(axiological)

It’s the contention of this note that the complex of questions surrounding environmental sustainability or creation care [2] provide a timely and appropriate integrative opportunity for mathematicians. This is because sustainability questions are at the same time quantitative questions (to say “sustainable” is to invite the questions: how long?, how much?, how do you measure?) and theological questions (to say “sustainable” is to invite the question what is worth sustaining? and how does it relate to the One who, according to Scripture (Hebrews 1:3; Colossians 1:17), “sustains everything by the word of his power”.) The diagram below (various versions of which can be found online by searching for “triple bottom line” or related phrases) suggests how sustainability can serve as an integrative or cross-cutting theme, even from a quite secular perspective.

sustainabilityA persistent line of argument in contemporary discourse (ranging from [14] in the 1960s to [1] this year) suggests that Christian faith has impeded a proper concern for the integrity of the created order. Addressing this claim will combine technical analysis with ontological, ethical and apologetic motifs to yield a powerful integrative theme.

2. A COURSE PROPOSAL

I teach at a large, secular school. My calling does not allow me to “integrate faith and learning” in a way that presumes or encourages student commitment to a particular faith tradition. Nevertheless, the preceding considerations have impelled me to develop a course proposal which will use “sustainability” as an integrative theme to press beyond the confines of a conventional mathematics course. I also feel that it’s important to offer this material to non science majors. Sustainability should be a showcase to students across the disciplines about the importance and value of a mathematical understanding. We’ll see how successful this is!

There is nothing surprising in wanting to develop a new course — it is what math professors do all the time. But usually, when I and my colleagues dream of new courses, we are thinking of small classes of eager graduate students to whom we can explain our latest research ideas. Here, I’m after something a bit different.

The goal will be through a General Education Mathematics course, to enable students to develop the quantitative and qualitative skills needed to reason effectively about environmental and economic sustainability. Let me unpack that a bit:

  • General Education Mathematics At most universities (including PSU), every student, whatever their major, has to take one or two ”quantitative” courses — this is called the ”general education” requirement. I want to reach out to students who are not planning to be mathematicians or scientists, students for whom this may be the last math course they ever take.
  • quantitative and qualitative skills I want students to be able to work with numbers (”quantitative”) – to be able to get a feeling for scale and size, whether we’re talking about gigatonnes of carbon dioxide, kilowatts of domestic power, or picograms of radioisotopes. But I also want them to get an intuition for the behavior of systems (qualitative), so that the ideas of growth, feedback, oscillation, overshoot and so on become part of their conceptual vocabulary.
  • to reason effectively A transition to a more sustainable society won’t come about without robust public debate — I want to help students engage effectively in this debate. I hope to do this partly by using an online platform for student presentations. Engaging with this process (which includes commenting on other people’s presentations as well as devising your own) will count seriously in the grading scheme.
  • environmental and economic sustainability I’d like students to get the mathematical idea that there are lots of scales on which one can ask the sustainability question—both time scales (how many years is ”sustainable”) and spatial scales. We’ll think about global-scale questions (carbon dioxide emissions being an obvious example) but we’ll try to look at as many examples as possible on a local scale (a single building, the Penn State campus, local agriculture) so that we can engage more directly.

We’ll address these goals through four general themes: Measuring (quantification and estimation), Changing (dynamical systems), Risking (probabilities), and Networking (graph theory ideas). It seems to me that these four
themes are the central ones in a mathematical understanding of ecology and of sustainability more broadly.

I am hoping to develop my own materials for this course. The following texts have, however, been an inspiration in various ways and anyone interested in developing a course of this kind might find it worth consulting one or more of them: [4], [5], [6], [7], [8], [13].

3. AN EXAMPLE

One does not have to develop a whole new course in order to use sustainability themes in mathematics education. Here is a simple example showing how a sustainability unit can be integrated within a calculus class. Many calculus examples are hackneyed (how often do you really prop a ladder against a wall with its foot in the bed of a truck driving at constant velocity?) The design of wind turbines provides the focus for a nice optimization problem in which the extrema of a cubic polynomial arise naturally. For more detail on this, see [3], Section 5.2.

Two key parameters govern the amount of energy available to a wind turbine: the area S swept out by the turbine blades, and the speed v1 of the incoming wind. A third relevant quantity is a constant, the air density ρ. In one second, a cylinder of air of cross-section S and length v1 approaches the turbine. The mass of this air is then ρSv1 and the kinetic energy it contains is half the mass times the square of the speed, that is

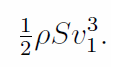energyThis is the power (energy per unit time) theoretically available in the cylinder of wind incident on the turbine.

But the turbine can’t possibly extract all that power! To understand why not, imagine what would happen if we extracted all the energy from some cylinder of the incoming wind. That cylinder of air would stop moving. Then, there would be nowhere for the next lot of incoming wind to go! So, while the air must slow down some as it passes the turbine and loses energy, it can’t slow down completely. How much of the theoretical power can we extract from the incoming wind?

An idealized wind turbine may be modeled as follows. Wind arrives from one side (say the left) the left at speed v1, passes through the turbine of area S at speed v(avg), and leaves at the right at speed v2. As the air slows down, it spreads out, because the total volume V of air (per unit time) passing each “slice” must be the same. That is, if A1 is the cross-sectional area of the cylinder of incoming air, and A2 that of the corresponding cylinder of outgoing air, we must have

volumeThe power available to the turbine is the difference between incoming and outgoing kinetic energies, that is,

powerIt can be shown (using conservation of momentum as well as energy; the details are in [3]) that v(avg) = 1/2 (v1 + v2). Thus the available power is

available powerwhere  λ = v2/v1.

In this equation, S and v1 are fixed, but the ratio λ between [0, 1] can be changed by varying the turbine design. What choice of  will make the energy output as great as possible?

It is a simple calculus exercise to show that the maximum value occurs when λ= 1/3 ; at this point

maximum valueand the maximum power available to the turbine is 16/27  or roughly 59% of the naive estimate

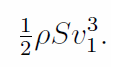energyThis is called the Betz limit on wind turbine efficiency.

Note. The MAA ran a workshop this spring aimed at developing a portfolio of freely accessible units on mathematics and sustainability; the above is based on one of my contributions to this workshop. The whole portfolio can be found at [10], see the URL http://serc.carleton.edu/sisl.

REFERENCES

[1] David C. Barker and David H. Bearce. End-Times Theology, the Shadow of the Future, and Public Resistance to Addressing Global Climate Change. Political Research Quarterly, 66(2):267–279, June 2013.

[2] Richard Bauckham. The Bible and Ecology: Rediscovering the Community of Creation. Baylor University Press, August 2010.

[3] Egbert Boeker and Rienk van Grondelle. Environmental Physics: Sustainable Energy and Climate Change. Wiley, 3 edition, September 2011.

[4] John Harte. Consider a Spherical Cow. University Science Books, June 1988.

[5] John Harte. Consider a Cylindrical Cow: More Adventures in Environmental Problem Solving. University Science Books, February 2001.

[6] Lee R. Kump, James F. Kasting, and Robert G. Crane. Earth System, The. Prentice Hall College Div, 1 edition, March 1999.

[7] Greg Langkamp and Joseph Hull. Quantitative Reasoning & the Environment. Pearson, 1 edition, July 2006.

[8] Robert L. McConnell and Daniel C. Abel. Environmental Issues: An Introduction to Sustainability. Benjamin Cummings, 3 edition, April 2007.

[9] Arlin Migliazzo. Teaching as an act of faith : theory and practice in church-related higher education. Fordham University Press, 1st ed. edition, 2002.

[10] Debra Rowe. Sustainability Improves Student Learning.

[11] Francis A Schaeffer, Udo Middelmann, Lynn White, and Richard L Means. Pollution and the death of man. Crossway Books, Wheaton, Ill., 1992.

[12] Paul Tillich. The Shaking of the Foundations:. Wipf & Stock Pub, reprint edition, May 2012.

[13] Martin E Walter. Mathematics for the environment. Chapman & Hall/CRC Press, London; Boca Raton, FL, 2011.

[14] Lynn White. The Historical Roots of Our Ecologic Crisis. Science, 155(3767):1203–1207, March 1967. PMID: 17847526.

Related Post: Stewards of the Created Order